Failing grade, or a C+? A tentative defense of the odds against chance "fallacy".

Let me start by saying that I really like Failing Grade: 89% of Introduction-to- Psychology Textbooks That Define or Explain Statistical Significance Do So Incorrectly. In this brief paper, Cassidy and colleagues examine how those who write introductory psychology textbooks define or describe statistical significance. Specifically, they look at the definition of statistical significance "most central to a reader's experience" - not all of the definitions (if there were more than one), or the only one. It's not meta-research, because it's not research on research, but it's close. It's a great piece of investigative journalism and it's on the teaching of statistics - a really important topic.

However, I want to focus here briefly on the authors describe as the "odds against chance" fallacy. That is, the seemingly incorrect assertion that "statistical significance means that the likelihood that the result is due to chance is less than 5%". This is worth focusing on because this was the most common "fallacy" - present in 80% of definitions.

I think this fallacy may, in some circumstances, rather be shorthand (a short and simple way of expressing something) designed for lay audiences; rather than a textbook writer's mistaken belief (a fallacy). I've recently realized people find technical definitions (the probability of the null given this or more extreme... etc) quite difficult. I think there is a real possibility that this definition represents an earnest attempt on the part of the textbook writers studied to communicate accessibly with statistical novices -- knowing that it is technically a bit rough around the edges. While a description like this may infuriate purists, it's possible that this what an accessible description of statistical significance looks like.

If I had been a reviewer on this paper, I might have suggested the authors reach out to the textbook writers and ask some quick questions. Why did you define it that way? Were you catering for an audience? And there's a comment in the discussion which leads me to believe the authors have an eye on this anyway. The authors say that their results "may also suggest that the odds-against-fallacy is a particularly tempting fallacy in the context of trying to communicate statistical significance to a novice audience". But is it a tempting "fallacy" (false belief) or convenient shorthand? I think this is an open question.

Moreover, if it is accessible shorthand, I think it's not that bad. Here is my defense: If the null is true, but we have observed a non-null, then this result can be said to have occurred "by chance". It's a false positive, coincidental, "chance". If (a) the p-value tells us something about how likely this or more extreme data is, if the null is true, and (b) we have a non-null and (c) our p-value is "small" then (d) it might be OK to say the likelihood it's due to chance is small (less than x%). We can talk about chance with something of a straight face. It's all a bit colloquial, it's all a bit loose, but it's not the end of the world. Is it a C+, perhaps, not an F? And hopefully students who move on from the introductory texts are taught something more concrete in due course. Hopefully.

Maybe I'm too soft, ill-informed, or missing something, but I don't think it's terrible. Anyway, all this is to say it's an interesting paper. But I think there's more to it.

A Function for Meng's Test of the Heterogeneity of Correlated Correlation Coefficients

Here's a first draft of a simple function for the test of heterogeneity of correlated correlation coefficients in Meng, Rosenthal and Rubin (1992), which I blogged about way back when. There are no tests included (e.g. tests that input is numeric) and the code is undoubtedly a bit flabby, but it works perfectly well.

It's a potentially useful test for many, but doesn't appear to be provided in any of the mainstream statistical software. 

Importantly, the function works for any number of correlated correlation coefficients and also allows for contrast tests. 

As input, the function takes a vector of correlations, the median correlation between the variables, sample size, and contrast weights (if required). 

I'm making an R package

I've got a rabble of functions that help me explore, analyse and quality assure the data I work with. My R skills are getting there. Sure there's room for (lots of) improvement, but all of my latest scripts are sufficiently less cringeworthy than my early attempts. I'm remembering to add na.rm = TRUE. 90% of the time, anyway. It's a perfect storm.

I'm making an R package? You know what, I think I am.

It's a (genuinely) exciting moment for me, but I thought I'd ask the good people of twitter if they had any advice before I really got going.

Finally took the plunge and started making my first R package today. Time to round up my herd of functions. Exciting! Anyone got any advice, anything you wish you’d known before you started yours? #rstats

— Adam Pegler (@pegleraj) 12 October 2018

Here's the advice I was given by those who know a thing or two.

(1) Maelle Salmon linked me to her excellent blogpost. She argues that, from the outset, an R package has to be potentially useful to others and novel. Oh, and make sure there isn't a similar one that already does the things your going to spend hours programming. If it isn't, and there is, don't bother. Sage advice in the "if ain't broke, don't fix it" mold.

(2) Daniel Lakens recommended this primer written by Karl Broman. Among other things, Karl reminds us that you needn't distribute a package to anyone; you're likely to benefit from bundling your functions even if the package never hits CRAN. Karl talks us through the whole process: building it, documenting it, testing it, choosing a software licence, and getting it on CRAN (if it gets that far).

(3) Matthew told me to

Usethis, devtools, and testthat make it easy to do things right.
Make sure you have no variables loose in your environment.
Have fun. pic.twitter.com/7s5rNXaCTY

— Mathew Ling (@lingtax) 13 October 2018

I like the last bit. Thanks, Mathew, I will!

Brenton Wiernik also encouraged me to write tests with testthat.

Write tests with testthat early and often

— Brenton Wiernik 🏳️‍🌈 (@bmwiernik) 13 October 2018

(4)  Tony said: "for god's sake don't write the essay the night before the deadline!" Sounds really sensible.

Don't save documentation for the end.

— Tony Rodriguez (@ttrodrigz) 13 October 2018

(5) Both Cedric and Danton recommended the devtools::load_all() function, Usethis, and restarting R intermittently. 

devtools::load_all() is very useful when you need to test something interactively. Usethis package is a time-saver!

— Cédric Batailler (@cedricbatailler) 13 October 2018

As you build functions in R/ directory, use devtools::load_all() to load into package environment and occasionally restart R to clear out existing function / objects. A big headache for me was that I’d finalize a function in R/ but it also existed in global env, which supercedes.

— Danton Noriega (@dantonnoriega) 13 October 2018

(6) Eric recommended this video with a short and snappy title: "you can make a package in 20 minutes". Sounds like rubbish to me - Jim! Appreciate the positive attitude, nonetheless.

Made my first package 2 weeks ago. Using the talk by @jimhester_ : https://t.co/mEdUjrxZIG Great instructions!

— Eric Krantz (@EricLeeKrantz) 14 October 2018

(7) And, last but by no means least, James gave a thumbs up to Hadley Wickham's book and an honorable mention to devtools and roxygen2:

I made my first package this week using @hadleywickham's great 'R packages' book https://t.co/atkeT6IlCm Also not sure I would have managed without #devtools and #roxygen2. Good luck!

— James Grecian (@JamesGrecian) 13 October 2018

So, to conclude, yes I am making an R package.

And I'll be taking the advice of the good people of twitter.

Many thanks to the people who responded to my tweet.

To Measure You Must First Define: Excerpts from Psychology

In an interesting and relatively recent article entitled Measurement is Fundamentally a Matter of Definition, Not Correlation, Krause (2012) claimed that psychologists typically pay little attention to defining the things they intend to measure. Instead, they primarily look to establish that putative measures of the concepts they are interested in have correlations with measures of other psychological variables that conform to prediction. This practice is ultimately a problem, Krause contends, because:

“It is only the conformity of a measure to the normative conceptual analysis and so definition of a dimension that can make the measurements it produces valid measurements on that dimension. This makes it essential for each basic science to achieve normative conceptual analyses and definitions for each of the dimensions in terms of which it describes and causally explains its phenomena.” (p. 1)

Given the overwhelming emphasis on statistics in introductory textbooks on scale construction, measurement validity, and psychometrics, I have a feeling that some will consider the idea that measurement is fundamentally a matter of definition rather revolutionary. It is likely to seem even more revolutionary given that many of articles referenced by Krause to support his viewpoint were fairly modern (e.g., Borsboom, 2005; Krause, 2005; Maruan, 1998*).

The point of this (admittedly, quite dry) blog post is to simply point out that, over the last century, a number of psychometricians argued that defining the variable was vital—the first step on the road to successful measurement. The collection of following quotations—all except Clark and Watson (1995) from texts not referenced by Krause—demonstrate this point.

“Measurement, of course, is only a final specialization of description. Measurement...can come in to its own only when qualitative description has truly ripened... no science has reached adult stage without passing through a well-developed descriptive stage” (Cattell, 1946, p. 4)

“Before we can validate the test we have to define the trait which it is designed to measure. Accurate qualitative description therefore has to precede measurement. In other words, psychology has to explore the characters of the unitary traits of man before mental testing can begin” (Cattell, 1948, p. 1)

“The definition of a variable provides the basis for the development of a series of operations that are to be performed in order to obtain descriptions of individuals in terms of the ways in which they manifest the particular property. The characteristics of the variable dictate the nature of the operations. With one variable there will be one series of operations, and with another variable a different series” (Ghiselli, 1964, p. 20)

“If a scale is to be developed to measure a common trait, the scale must contain items. And before the items can be written, the trait or construct that the items will presumably measure must be defined. It is necessary, in other words, to make explicit the nature of the trait or construct that we hope to measure.” (Edwards, 1970, p. 29)

“A measure should spring from a hypothesis regarding the existence and nature of an attribute” (Nunnally, 1970, p. 213)

“We cannot measure well when we cannot specify clearly what we are trying to measure, where it occurs, and when” (Fiske, 1971, p. 30)

“We cannot measure a variable well if we cannot describe it” (Fiske, 1971, p. 117)

“To advance the science of personology, intensive effort must be devoted to each major construct, to delineating it explicitly and systematically, and to create measuring procedures conforming to the blueprints derived from such a conceptualization” (Fiske, 1971, p. 144)

“Let us try to learn to be free from other a priori mathematical and statistical considerations and prescriptions – especially codes of permission. Instead, let us try to think substantively during the initial stages of measurement, and focus directly on the specific universe of observations with which we wish to do business” (Guttman, 1971, p. 346)

“Lazarsfield and Barton (1951) have described the process of measurement in the social sciences in terms of four progressive stages. The first stage they describe is one in which the investigator forms an initial image of the nature of the concept he wishes to measure” (Lemon, 1973, p. 29)

“...the construct definition sets the boundaries for potential measurement techniques. It operates like a test plan for the development of an instrument” (Shavelson, Hubner, & Stanton, 1976, p. 415)

“...the first problem that the psychologist or educator faces as he tries to measure the attributes that he is interested in is that of arriving at a clear, precise, and generally accepted definition of the attribute he proposes to measure” (Thorndike & Hagen, 1977, p. 10)

“A less obvious, but equally important, characteristic shared by enumeration and measurement is that they both require prior definition. We cannot reliably quantify without first defining the objects of properties to be quantified” (Gordon, 1977, p. 2)

“a meaningful and essential question to raise about a measure is whether it is consistent with the definition of the construct it is meant to be tapping” (Pedhazur & Pedhazur-Schmelkin, 1991, p. )

“A critical first step is to develop a precise and detailed conception of the target construct and it theoretical context. We have found that writing out a brief, formal description of the construct is very useful in crystallizing one’s conceptual model” (Clark & Watson, 1995, p. 310)

“Carefully define the domain and facets of the construct and subject them to content validation before developing other elements of the assessment instrument... a construct that is poorly defined, undifferentiated, and imprecisely partitioned will limit the contend validity of the assessment instrument” (Haynes, Richard, & Kubany, 1995, p. 244)

“To summarize, I offer a five-step model for construct validity research (depicted in Figure 1 and heavily influenced by Meehl, 1978, 1990a). The steps are (1) careful specification of the theoretical constructs in question...” (Smith, 2005, p. 399)

“Every new instrument (or even the redevelopment or adaptation of an old instrument) must start with an idea – the kernel of the instrument, the “what” of the “what does it measure?” and the “how” of “how will the measure be used?” (Wilson, 2005, p. 19)

“The measurement of concepts like creativity and intelligence is limited by the clarity with which we are able to define the meaning of these constructs...” (Rust & Golombuk, 2009, p. 31)

“Concepts are the starting point in measurement. Concepts refer to ideas that have some unity or something in common. The meaning of a concept is spelled out in a theoretical definition.” (Bollen, 2011, p. 360)

“Theory enters measurement throughout the process. We need theory to define a concept and to pick out its dimensions. We need theory to develop or to select indicators that match the theoretical definition and its dimensions. Theory also enters in determining whether the indicator influences the latent variable or vice versa.” (Bollen, 2011, p. 361)

“The first, and perhaps most deceptively-simple, facet of scale construction is articulating the construct(s) to be measured. Whether the construct (one or more) is viewed as an attitude, a perception, an attribution, a trait, an emotional response, a behavioural response, a cognitive response, or a physiological response, or-more generally, a psychological response, tendency, or disposition of any kind—it must be carefully articulated and differentiated from other constructs” (Furr, 2011, p. 12)

"The first stage of the scale development and validation process involves defining the conceptual domain of the construct" (MacKenzie, Podsakoff, & Podsakoff, 2011, p. 298).“The topic of conceptualization of measurement variables is probably the least quantitative of the fields of study. Psychometricians have typically shied away from this area of our work, possibly for this exact reason. Yet, it is the most important, for without adequate conceptualization, all else is empty-in particular the whole concept of “validity evidence” becomes moot, as there is no substance to validate to” (Wilson, 2013, p. 222)

* See Krause's references for these references. Sorry!

References

Bollen, K. A. (2011). Evaluating effect, composite, and causal indicators in structural equation models. MIS Quarterly, 35(2), 359-372.

Edwards, A. L. (1970). The measurement of personality traits by scales an inventories. New York: Holt, Rinehart, and Winston.

Cattell, R. B. (1946). Description and measurement of personality. London: George G. Harrap & Co.

Fiske, D. W. (1971). Measuring the concepts of personality. Oxford, England: Aldine.

Furr, R. M. (2011). Scale construction and psychometrics. London: Sage.

Ghiselli, E. E. (1964). Theory of psychological measurement. New York: McGraw-Hill.

Gordon, R. L. (1977). Unidimensional scaling of social variables: Concepts and procedures. New York: The Free Press.

Guttman, L. (1971). Measurement as structural theory. Psychometrika, 36(4), 329-347.

Haynes, S. N., Richard, D. C. S., & Kubany, E. S. (1995). Content validity in psychological assessment: A functional approach to concepts and methods. Psychological Assessment, 7(3), 238-247.

Krause, M. S. (2012). Measurement validity is fundamentally a matter of definition, not correlation. Review of General Psychology, 16(4), 391-400. http://dx.doi.org/10.1037/a0027701

Lemon, N. (1973). Attitudes and their measurement. London: C. Tinling & Co

Nunnally, J. C. (1970). Introduction to psychological measurement. New York: McGraw-Hill.

Pedhazur, E. J., & Schmelkin, L. P. (1991). Measurement, design, and analysis: An integrated approach. New York, NY: Psychology Press.

MacKenzie, S. B., Podsakoff, P. M., & Podsakoff, N. P. (2011). Construct measurement and validation procedures in MIS and behavioral research: Integrating new and existing techniques. MIS quarterly, 35(2), 293-334.

Rust,  J., & Golombok, S. (2009). Modern psychometrics: The science of psychological assessment. London: Routledge.

Shavelson, R. J., Hubner, J. J., & Stanton, G. C. (1976). Self-concept: Validation of construct interpretations. Review of Education Research, 407-441.

Smith, G. T. (2005). On construct validity: Issues of method and measurement. Psychological Assessment, 17(4), 396-408.

Thorndike, R. L., & Hagen, E. P. (1977). Measurement and evaluation in psychology and education. New York: John Wiley and Sons. 4^th edition

Wilson, M. (2005). Constructing measures: An item response modelling approach. London: Lawrence Erlbaum Associates.

Wilson, M. (2013). Seeking a balance between the statistical and scientific elements in psychometrics. Psychometrika, 78(2), 211-236.

R Code for Plotting Power by N by Alpha

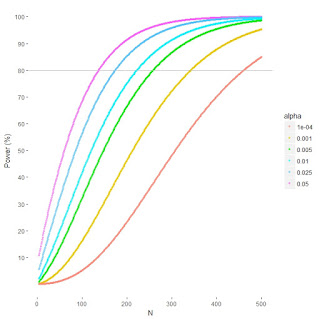
I tweeted a couple of scatterplots today. One shows the relationship between N and power, for 6 alpha levels. I don't know why I made it, really. I'd recently cracked some code for automating power estimates with the pwr package in R and I had a day off so I thought I'd put it to use. It might be of interest to anyone with an interest in the recent alpha debates. It displays power for the average effect size in personality and social psychology (r = .21) by N by alpha. The takeaway from the graph is that N needs to increase as alpha decreases. This is all totally unsurprising, of course, and usual caveat about power being a highly theoretical concept applies.

Anyway. The code is below. It can be modified quite easily, I expect, to help answer other questions. Change rs, alphas, Ns, to investigate other things.

Converting a Correlation Matrix to a Covariance Matrix with Lavaan

Researchers are sometimes interested in converting a correlation matrix in to a covariance matrix.  Perhaps they happen to use statistical software or an R package that can deal with covariance matrices as input, but not correlation matrices (e.g., the fantastic SEM package Lavaan (Rosseel, 2012), or the first step of the two-step meta-analytic SEM method implemented in the metaSEM package (Cheung, 2015). Or perhaps they are just inexplicably inquisitive and/or enjoy wasting hours performing pointless transformations.

Conveniently, the fantastic Lavaan has a built-in function for converting a correlation matrix in to a covariance matrix (others probably do too, but I don't know about them: forgive me). I'm going to show you how to use that function here because the Lavaan documentation does not show you how to use it in any real detail (as far as I can see).

First, you need to provide the correlation matrix. Simply duplicate the matrix that appears in the paper that you're interested in. For example, the one below from my friend Jennifer's paper on spitefulness and humor styles.

It needs to be symmetric, so you should fill upper and lower triangles of the matrix, in addition to a correlation of 1 for the variable with itself.

Use this code (it looks a lot better in the gist embedded below):

corr1 <- matrix(c(  1, -.47, -.16, -.18, -.26,
                    -.47,  1,   .07,  .04,  .36,
                    -.16, .07,   1,  -.13, -.10,
                    -.18, .04, -.13,   1,   .19,
                    -.26, .36, -.10,  .19,   1), nrow = 5, ncol = 5, byrow = FALSE)


The highlighted matrix and the code below should make it easier to identify from where the coefficients should be drawn and where they should go. Follow the colours.

Second, you need provide the standard deviations for each column (each variable, item, etc.).

Look at the SDs (above) and put them in the code below (in order!):

corr1sd = c(.65, .62, .68, .68, .66)

Third, you can perform the transformation using Lavaan's cor2cov function:

cov1 <- cor2cov(corr1, sds = corr1sd)

And there you have it. Covariances and variances on the diagonal. You can take this matrix forward in to a package that deals with it, such as metaSEM. Or you can play with it a bit and take in to Lavaan (blog to come on how to transform this matrix so it can be used in Lavaan or metaSEM).




Cheung, M. W. L. (2015). {metaSEM}: An R Package for Meta-Analysis using Structural Equation Modeling. Frontiers in Psychology. http://journal.frontiersin.org/article/10.3389/fpsyg.2014.01521/full 

Yves Rosseel (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2), 1-36. URL http://www.jstatsoft.org/v48/i02/

80% power for p < .05 and p < .005

In the last few months there has been a new round of debate on p values. Redefine statistical significance by Benjamin et al. (2017) kicked things off. In that article the authors argued that "for research communities that continue to rely on null hypothesis significance testing, reducing the P-value threshold for claims of new discoveries to 0.005 is an actionable step that will immediately improve reproducibility" (p. 11). Fisher's arbitrary choice of 0.05 is no longer adequate.

To be clear, Benjamin et al., did state that their recommendations were specifically for "claims of discovery of new effects" (p. 5). But imagine a scenario where 0.005 is the new 0.05, for all research.

What happens to my 80% power sample sizes if I switch to the new alpha level? How much larger will the sample need to be? For one-sided tests of Pearson's r to 2dps, the answers appear in the table below.

In brief, for correlational research, switching from .05 to 0.005 will require you multiply your sample size by around 1.82 (that's the median figure). Stated differently, that's an 82% increase in participants.

r	.05	.005	Increase in N	Multiply N by (2dp)
.01	61824	116785	54961	1.89
.02	15455	29193	13738	1.89
.03	6868	12972	6104	1.89
.04	3862	7295	3433	1.89
.05	2471	4667	2196	1.89
.06	1716	3239	1523	1.89
.07	1260	2379	1119	1.89
.08	964	1820	856	1.89
.09	762	1437	675	1.89
.10	617	1163	546	1.88
.11	509	960	451	1.89
.12	428	806	378	1.88
.13	364	686	322	1.88
.14	314	591	277	1.88
.15	273	514	241	1.88
.16	240	451	211	1.88
.17	212	399	187	1.88
.18	189	356	167	1.88
.19	170	319	149	1.88
.20	153	287	134	1.88
.21	139	260	121	1.87
.22	126	236	110	1.87
.23	115	216	101	1.88
.24	106	198	92	1.87
.25	97	182	85	1.88
.26	90	168	78	1.87
.27	83	155	72	1.87
.28	77	144	67	1.87
.29	72	134	62	1.86
.30	67	125	58	1.87
.31	63	117	54	1.86
.32	59	109	50	1.85
.33	55	102	47	1.85
.34	52	96	44	1.85
.35	49	90	41	1.84
.36	46	85	39	1.85
.37	44	80	36	1.82
.38	41	76	35	1.85
.39	39	72	33	1.85
.40	37	67	30	1.81
.41	35	65	30	1.86
.42	33	61	28	1.85
.43	32	58	26	1.81
.44	30	55	25	1.83
.45	29	53	24	1.83
.46	28	50	22	1.79
.47	26	48	22	1.85
.48	25	46	21	1.84
.49	24	44	20	1.83
.50	23	42	19	1.83
.51	22	40	18	1.82
.52	21	38	17	1.81
.53	20	37	17	1.85
.54	20	35	15	1.75
.55	19	34	15	1.79
.56	18	32	14	1.78
.57	17	31	14	1.82
.58	17	30	13	1.76
.59	16	29	13	1.81
.60	16	27	11	1.69
.61	15	26	11	1.73
.62	14	25	11	1.79
.63	14	24	10	1.71
.64	13	23	10	1.77
.65	13	23	10	1.77
.66	13	22	9	1.69
.67	12	21	9	1.75
.68	12	20	8	1.67
.69	11	19	8	1.73
.70	11	19	8	1.73
.71	11	18	7	1.64
.72	10	17	7	1.70
.73	10	17	7	1.70
.74	10	16	6	1.60
.75	9	16	7	1.78
.76	9	15	6	1.67
.77	9	14	5	1.56
.78	9	14	5	1.56
.79	8	13	5	1.63
.80	8	13	5	1.63
.81	8	12	4	1.50
.82	8	12	4	1.50
.83	7	12	5	1.71
.84	7	11	4	1.57
.85	7	11	4	1.57
.86	7	10	3	1.43
.87	6	10	4	1.67
.88	6	10	4	1.67
.89	6	9	3	1.50
.90	6	9	3	1.50
.91	6	8	2	1.33
.92	6	8	2	1.33
.93	5	8	3	1.60
.94	5	7	2	1.40
.95	5	7	2	1.40
.96	5	7	2	1.40
.97	5	6	1	1.20
.98	—	6
.99	—	5

Note. Sample size information computed using R package pwr, using variations on the following code

pwr.r.test(n = , r = , sig.level = 0.05, power = .80, alternative = "greater")